This is one of the most fascinating things I've ever encountered in math: fractals. Fractals are essentially self-repeating patterns. Kind of like cutting a piece of string in half, then each new piece in half, then each of those, ad infinitum. It's theoretically possible to do this forever without end.
The pictures below are the graphical representation of the equation f(z) = z2+c, where z is a complex number. We start with z=0+0i, and look for complex numbers c, such that 0, f(0), f[f(0)], and so on, remain bounded.
If you think that I understand everything I just said, think again. I get the idea of iteration, and plugging the result of the function back into the function over and over again. But the complex number stuff eludes me. Anyhoo, the neat thing is the graphical result.

Here's the whole set. The colours represent different numbers of iterations (I think). See where that arrow is? That's where we zoom into for the next picture.

See what I mean by 'self-replicating'? But it's not quite that boring. We zoom in on the arrow again...
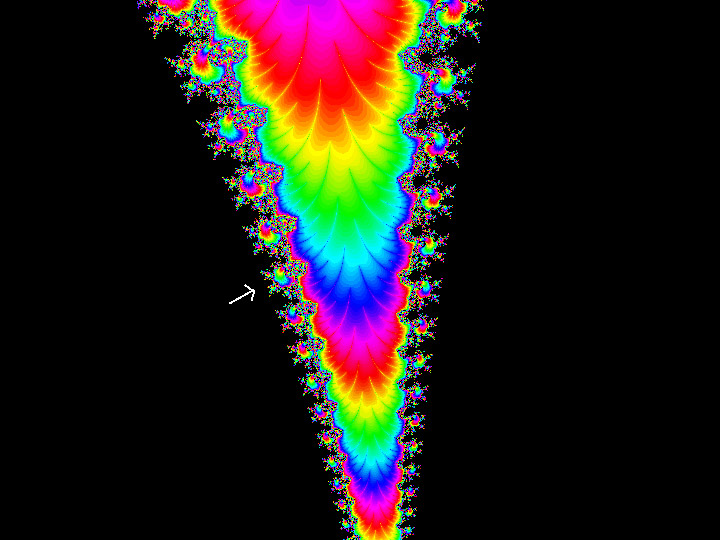
Now the edges of the black are looking a little bit different...

And look at this. Beautiful. You can keep zooming in as many times as you like. Literally infinitely. And you could find different swirls and patterns forever. Depending on how close you look, at how many iterations, at what point on the real-complex plane, you'll see something new every time.
It was this piece of math that first made me say, Somewhere in here are the mysteries of God.
